Question 1, Exercise 10.2

Solutions of Question 1 of Exercise 10.2 of Unit 10: Trigonometric Identities of Sum and Difference of Angles. This is unit of A Textbook of Mathematics for Grade XI is published by Khyber Pakhtunkhwa Textbook Board (KPTB or KPTBB) Peshawar, Pakistan. There are four parts in Question 1.

Find the value of $\sin 2\theta ,\,\,\cos 2\theta$ and $\tan 2\theta$, given $\tan \theta =-\dfrac{1}{5}$, $\theta$ in quadrant II.

By drawing the reference triangle as shown:

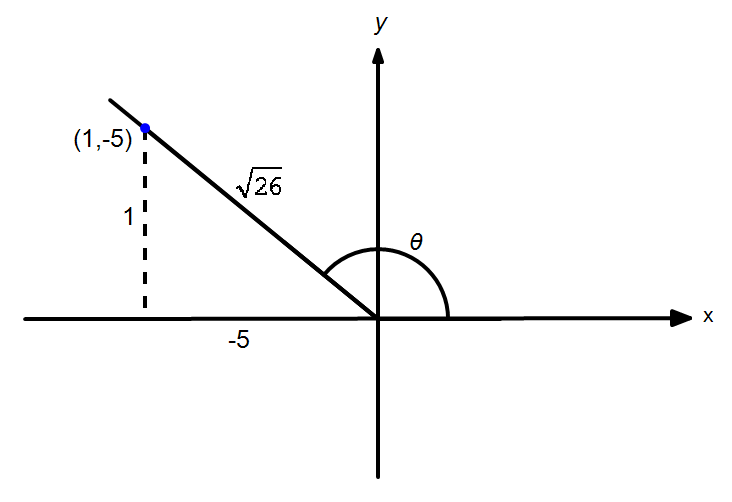
we find $\sin \theta =\dfrac{1}{\sqrt{26}}$ and $\cos \theta =\dfrac{-5}{\sqrt{26}}$ Thus, we have the following by using double angle identities. $$\begin{align}\sin 2\theta &=2\sin \theta \cos \theta \\ &=2\left( \dfrac{1}{\sqrt{26}} \right)\left( \dfrac{-5}{\sqrt{26}} \right)\\ &=-\dfrac{10}{26} \end{align}$$ $$\implies \bbox[4px,border:2px solid black]{\sin 2\theta=-\dfrac{5}{13}}$$ $$\begin{align}\cos 2\theta &={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \\ &={{\left( \dfrac{-5}{\sqrt{26}} \right)}^{2}}-{{\left( \dfrac{1}{\sqrt{26}} \right)}^{2}}\\ &=\dfrac{25}{26}-\dfrac{1}{26}=\dfrac{24}{26}\end{align}$$ $$\implies \bbox[4px,border:2px solid black]{\cos2\theta=\dfrac{12}{13}}$$ $$\begin{align}\tan 2\theta &=\dfrac{\sin 2\theta }{\cos 2\theta }=\dfrac{\frac{-5}{13}}{\frac{12}{13}}\end{align}$$ $$\implies \bbox[4px,border:2px solid black]{\tan 2\theta=-\dfrac{5}{12}}$$

Question 2 >