Question 3, Exercise 10.2

Solutions of Question 3 of Exercise 10.2 of Unit 10: Trigonometric Identities of Sum and Difference of Angles. This is unit of A Textbook of Mathematics for Grade XI is published by Khyber Pakhtunkhwa Textbook Board (KPTB or KPTBB) Peshawar, Pakistan.

If $\sin \theta =\dfrac{4}{5}$ and terminal ray of $\theta$ is in the second quadrant, then find $\sin2\theta$.

Given: $\sin \theta =\dfrac{4}{5}$

Terminal ray of $\theta$ is in the second quadrant and by drawing the reference triangle as shown:

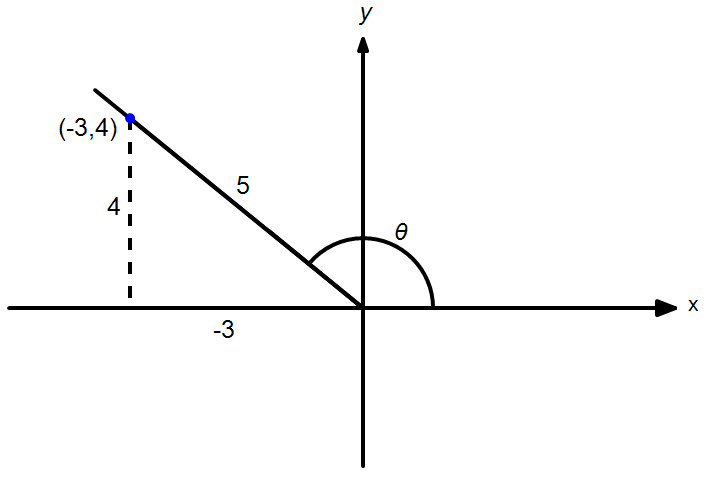
We find: $\cos \theta =-\dfrac{3}{5}$.

Thus, we have the following by using double angle identity: $$\begin{align}\sin 2\theta &=2\sin \theta \cos \theta \\ &=2\left( \dfrac{4}{5} \right)\left( -\dfrac{3}{5} \right)\end{align}$$ $$\implies \bbox[4px,border:2px solid black]{\sin 2\theta=-\dfrac{24}{25}.}$$

If $\sin \theta =\dfrac{4}{5}$ and terminal ray of $\theta$ is in the second quadrant, then find $\cos \dfrac{\theta }{2}$.

Given: $\sin \theta =\dfrac{4}{5}$

Terminal ray of $\theta$ is in the second quadrant and by drawing the reference triangle as shown:

We find: $\cos \theta =-\dfrac{3}{5}$.

Thus, we have the following by using half angle identities: $$\begin{align}\cos \dfrac{\theta }{2}&=\sqrt{\dfrac{1+\cos \theta }{2}}\\ &=\sqrt{\dfrac{1-\dfrac{3}{5}}{2}}=\sqrt{\dfrac{2}{10}}\end{align}$$ $$\implies \bbox[4px,border:2px solid black]{\cos \dfrac{\theta }{2}=\dfrac{1}{\sqrt{5}}}$$

< Question 2 Question 4 >